Regioseletividade na Reação de Diels-Alder

Nessa prática será usado o nível de teoria semi-empíricio PM3 para estudar uma variedade de reações de Diels-Alder. Será necessário executar as seguintes etapas:

1. Otimizar as geometrias dos reagentes: etileno, butadieno, acrilonitrila e isopreno.
2. Otimizar a geometria do cicloaduto Diels-Alder mais simples: ciclohexeno.
3. Encontrar o estado de transição correspondente.
4. Calcular as freqüências vibracionais para o estado de transição.
5. Estimar as propriedades termodinâmicas e cinéticas.
   
6. Otimizar a geometria dos outros 3 cicloadutos: 4-cianociclohexeno, 4-ciano-1-metil-ciclohexeno e 4-ciano-2-metil-ciclohexeno.
7. Otimizar os estados de transição substituídos.
8. Por fim, interpretar os resultados.
   

Geometrias dos Reagentes

A primeira etapa é a otimização da geometria dos reagentes (etileno, butadieno, acrilonitrila e isopreno). Primeiro, é nessário montar as moléculas no programa MOLDEN, e salvá-las no formato de Matriz-Z para o progama GAMESS. Usando o editor PFE edite o arquivo de entrada, input, para o programa GAMESS. Esse arquivo de entrada deve ter a seguinte estrutura: 

 $CONTRL RUNTYP=OPTIMIZE COORD=ZMT $END 
 $STATPT NSTEP=150 HESS=CALC HSSEND=.T. $END
 $BASIS GBASIS=PM3 $END
 $DATA
(nome do cálculo)
C1 (especificação da geometria)
 $END (obs: apague apenas os textos 'variables' e 'constants', não excluindo a linha. Além disso, deve haver um espaço em branco na primeira coluna de cada linha)

Depois é só rodar o cálculo executando o comando:

C:\DINAMICA\GAMESS.EXE -I EST01.INP -O EST01.OUT

Ele deve durar apenas alguns segundos, gerando um arquivo de saída, output, chamado, nesse caso, de EST01.OUT. Quando o cálculo terminar deve-se extrair a energia total, e verificar a geometria resultante. Para visualizar a geometria, abra o programa MOLDEN, clique em "Read", e selecione o arquivo de saída, output. Para verificar as geometrias que foram obtidas até a convergência, clique em "Geom. conv." e/ou no botão "Movie".

Algumas notas importantes:

• Hartrees (ou unidades atômicas) equivalem a 2625,5 kJ/mol. Para evitar erros numéricos adicionais nos resultados, use todos os decimais gerados pelo cálculo na conversão da energia total.
• Na otimização da geometria, a energia relevante é a da geometria final, após o texto ***** EQUILIBRIUM GEOMETRY LOCATED ***** (o cálculo convergiu), onde se lê "TOTAL ENERGY".
• Para calcular a energia de ativação para o estado de transição da reação deve-se considerar a energia do ponto zero. Esse resultado aparece depois do resultado para a geometria no equilíbrio, logo abaixo do texto  "THE HARMONIC ZERO POINT ENERGY IS ".
  
• Butadieno e Isopreno têm dois rotâmeros, que diferem nos ângulos diédros ao redor da ligação C--C central. A estrutura trans é mais estável. Otimize as duas estruturas e obtenha as energias de ativação.

Para montar o arquivo de entrada, input, para Etileno:

1.Rode o programa MOLDEN:    C:\DINAMICA\MOLDEN.EXE
2. Clique no botão "Label" e selecione "atom+number"
3. Clique em "ZMAT Editor"
4. Na nova janela "Zmatrix Editor" que se abre, clique em "Add Line"
5. Clique no botão "Double", em seguida clique no átomo de carbono da janela da tabela periódica que se abre
6. Clique em "Add Line"
7. Antes de marcar o segundo átomo de carbono, clique no botão "Double", em seguida clique no átomo de carbono, e clique em C(1) na tela que representa o átomo de carbono
8. Clique em "Add Line"
9. Antes de marcar o átomo de hidrogênio, clique no botão "Single", em seguida no átomo de hidrogênio, clique em C(1) e em C(2)
10. Clique em "Add Line"
11. Clique no átomo de hidrogênio da tabela periódica, em seguida clique em C(1), C(2) e H(3)
12. Continue até completar a estrutura H2C=CH2
13. Salve o arquivo digitando o nome do arquivo, p.ex. EST01.INP, no campo "File name?"
14. Clique "Write Z-Matrix"

Cyclohexeno

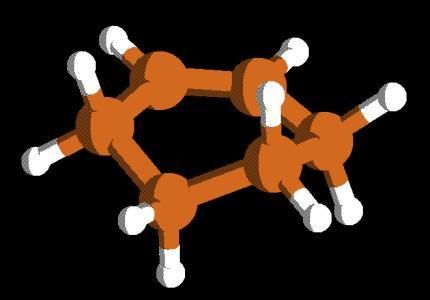
Agora otimize a estrutura do ciclohexeno. Existem várias conformações. A mais estável é similar à figura abaixo:

Essa molécula pode ser montada no programa MOLDEN conforme os passos abaixo:

1. Rode o programa MOLDEN:     C:\DINAMICA\MOLDEN.EXE
2.Clique em:
     ZMAT Editor
    Add Line
    C <átomo de carbono na Tabela Periódica>
    Substitute Atom by Fragment
    -CycloHexane)
3.Clique no último átomo de hidrogênio da matriz Z, e clique em "Delete Line". 
4.Salve o arquivo digitando o nome do arquivo, p.ex. TESTE01.INP, no campo "File name?"
5.Clique "Write Z-Matrix"

Clique aqui para voltar ao topo da página.

O Estado de Transição Diels-Alder Mais Simples

Encontrar o estado de transição para uma reação não é uma tarefa simples e requer alguma experiência com programas de Química Computacional, como o GAMESS. Eu recomendo que você copie a geometria do atalho:

• Etileno + Isobuteno
  

Caso você queira tentar encontar a geometria por conta própia, a figura abaixo é uma aproximação de como deve ser o estado de transição:

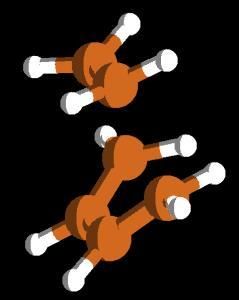
Usando (bastante) o MOLDEN, você poderá montar uma estrutura similar. Então, salve o arquivo, e edite o arquivo de entrada para o GAMESS. Esse arquivo deve ter a seguinte estrutura:

$CONTRL RUNTYP=SADPOINT COORD=ZMT $END
$STATPT NSTEP=150 HESS=CALC HSSEND=.T. $END
$BASIS GBASIS=PM3 $END
$DATA
(nome do cálculo)
C1
(especificação da geometria)
$END
(obs: deve haver um espaço em branco na primeira coluna de cada linha)

Alguns detalhes desse arquivo de entrada:

• RUNTYP=SADPOINT: Cálculo para localizar o estado de transição (SADle POINT = Ponto de Cela)
  
• HESS=CALC: calcular a matriz de constante de força, ou HESSiana.

Uma vez obtido o estado de transição, você pode comparar essa energia com a dos reagentes e obter uma energia de ativação teórica. Lembrar: as energias estão em unidades atômicas, sendo 1 u.a. = 1 Hartree = 2625,5 kJ/mol.

Clique aqui para voltar ao topo da página.

Cálculo das Freqüências Vibracionais

O cálculo das freqüências vibracionais já foi realizado nos cálculos dos reagentes e do estado de transição, com a inclusão do campo HSSEND=.T. nos arquivos de entrada. Isso significa o cálculo da matriz de constantes de força, Hessiana, após a otimização da geometria. No entanto, para visualizar as freqüências vibracionais, deve-se fazer um novo cálculo, seguindo o procedimento:

Feito isso, edite o arquivo TS01-F.INP com a seguinte estrutura:

 $CONTRL RUNTYP=HESSIAN COORD=ZMT $END
 $BASIS GBASIS=PM3 $END
 $DATA
(nome do cálculo)
C1
(especificação da geometria)
 $END
(obs: deve haver um espaço em branco na primeira coluna de cada linha)

Para visualizar as freqüências vibracionais e, por exemplo, confirmar se existe uma freqüência imaginária característica no estado de transição que representa a passagem de reagentes a produtos, siga a seqüência:

1. Abra o arquivo de saída TS01-F.OUT no programa MOLDEN
2. No campo "Frequencies:" clique no botão "Norm. Mode"
3. Vai aparecer uma nova janela com os valores das freqüências vibracionais harmônicas. Clicando nesses valores resultará no movimento vibracional característico para cada
freqüência. Analise a freqüência imaginária (o primeiro valor)
4. Para verificar, olhe essa animação do modo vibracional da freqüência imaginária para o estado de transição da cicloadição Etileno + Isobuteno

Cicloadutos Substituídos

Otimize as geometrias dos vários cicloadutos obtidos a partir dos reagentes substituídos: acrilonitrila e isopreno. Especificamente, você deve otimizar as geometrias dos adutos acrilonitrila/butadieno, e as dos dois adutos isoméricos acrilonitrila/isopreno. A melhor forma de gerar essas geometrias para esses cálculos é fazer o seguinte:

1. Abra o arquivo de saída, .OUT, do ciclohexeno menos substituído no MOLDEN
2. Adicione o subsitituinte usando as ferramentas dentro do botão "ZMAT Editor"
3. Salve as estruturas modificadas
4. Altere esse arquivo usando um editor de texto
5. Rode o cálculo no PCGAMESS.

Note que você deve colocar o grupo ciano em uma posição pseudo-equatorial.

Clique aqui para voltar ao topo da página.

Estados de Transição Substituídos

Assim como para os adutos substituídos do ciclohexeno, acima, a melhor forma de iniciar uma otimização de geometria para os estados de transição substituídos e modificar a geometria dos estados de transição convergidos para os estados menos substituídos. Uma vez convergido o estado de transição para uma determinada reação, você pode adicionar o grupo ciano para gerar uma geometria inicial para a reação acrilonitrila + butadieno. Então, quando o estado de transição convergir, adicione um grupo metila na posição meta ou para para gerar a geometria inicial para os dois estados de transição isoméricos para a reação acrilonitrila + isopreno.

Assim como para a reação original, você precisará calcular a matriz de constantes de forças, Hessiana, na geometria inicial.

Nota Importante: Para esses estados de transição, uma nova forma de isomerismo ocorre: o grupo ciano pode ser endo ou exo. Enquando que o produto final no caso considerado aqui não é alterado, a altura da barreira será diferente para os dois modos de aproximação. Aqui você deve considerar apenas os isômeros endo.

Clique aqui para voltar ao topo da página.

Interpretando os Resultados

Nesse ponto, você já deve ter feito:

• Obtenção das energias e geometrias de todos os reagentes, produtos e estados de transição.
• Calculado as freqüências vibracionais dos estados de transição.

Algumas questões para serem trabalhadas:

• É possível definir uma ordem de ligação parcial como exp(-(r - r₀)/a), onde a é uma constante igual a 0,35 Angstrom, e r₀ é o comprimento da ligação de equilíbrio para uma ligação simples típica entre os elementos considerados. Considerando r₀(C-C) = 1,54 Angstrom, use essa equação e  calcule as ordens de ligação parcial para todas as ligações C-C no eteno, butadieno e no ciclohexeno. Comente os valores obtidos.
• Calcule as odens de ligação parcial para todas as ligações C-C no estado de transição da reação original. Comente os valores obtidos.
• O que isso significa na reação original? Ela é síncrona?
• A animação do autovetor da freqüência imaginária no estado de transição sugere que o estado de transição encontrado é de fato aquele para a reação de Diels-Alder?
• Como se parecem os estados de transição substituídos? Calcule as ordens de ligação parcais para as novas ligações C-C formadas no estado de transição?
• Quais são as energias de ativação para todas as reações?
  
• Como as diferenças nas alturas das barreiras nos dois estados de transição isoméricos isopreno/acrilonitrila se ajustam com o resultado experimental (os produtos meta e para são formados em uma mistura isomérica na proporção 21,8 a 78,2% a 20 graus Célsius)? Considere que as constantes de velocidade são dadas pela expressão de Arrhenius , k=A*exp(-Ea/RT), e que as duas reações isoméricas têm o mesmo fator pré-exponencial. Lembre-se que a teoria PM3 fornece apenas valores aproximados!

Clique aqui para voltar ao topo da página.